量子系統的模擬

量子物理複習

量子物理複習

非時變性薛丁格方程：一維系統的本徵值與本徵態（束縛態）

對於位勢不隨時間而改變的薛丁格方程式，我們已經知道它是可以被改寫簡化成（時間變數分離出來）為一個本徵值型的二階微分方程式

- h²/2m ▽² ψ(x) + V(x)ψ(x) = Eψ(x)

注意其中 E 與 ψ(x) 皆為未知。當我們要用電腦計算的方法來求一個微分方程的數值解，就是等於要積分上式中帶有微分符號的部分，使未知函數變為已知。

這樣的一個問題裏，會出現兩種大不相同的解的型式，一是散射態、二是束縛態，在束縛態時最重要會出現的現象就是能量的量子化，也就是只有某些特定的能量值才是允許的。從計算的角度而言，允許與有是怎樣表現出來呢？是波函數能否被歸一化的基本要求。如果在某一個 E 值的試作下波函數發散了，它就沒有辦法被求出對整個空間的積分（無限大），因而也就沒有辦法歸一化它的波函數了。我們就認定這樣的 E 值是不允許的能量值，並且作其他的猜測，儘可能找出所有允許的 E 值與其對應的波函數解。

在本節為了利於模擬示範以上說明的特性，我們採用了一個較為簡化了的情況，就是只處理 V(-x) = V(x) 這種以 y=0 為鏡面對稱這種型式的一維位勢。這樣的對稱性將保證其解必有明確的宇稱性（parity），意思就是說其解必定是奇函數 f(-x) = -f(x) 或是偶函數 f(-x) = f(x) ，不會有其他的狀況。

這樣的特例帶給我們以下計算上的簡化：一、解自動分為奇函數與偶函數兩組，都只要處理後從零到正無限大之間的範圍求解即可（因奇偶函數的另一半是確定的），另外，凡奇函數者皆可由初始原點以 f(x=0) = 0、f'(x=0) = 1 作初始條件出發開始向右積分，而偶函數者皆可由初始原點以 f(x=0) = 1、f'(x=0) = 0 作初始條件出發開始向右積分。

要積分的方程式，經整理後有以下型式

d²/dx² ψ(x) = 2m/h² [V(x) -E]ψ(x)

可化化為兩個聯立的一階常微方式：

d/dxψ(x) = ψ' (x)

d/dx ψ' (x) = 2m/h² [V(x) -E]ψ(x)

注意參考書上建議用下面這種 Euler-Cromer 演算法來處理這種會振盪的解就夠好了（詳見參考書課文），也就是

f'_s+1 = f'_s + f''_s+1 Dx

f_s+1 = f_s + f'_s+1 Dx

我們也因此不必動用像 Runge-Kutta 那種較高階且較精密的演算法（詳見數值方法線上教材）。另外，若我們採行所謂的原子單位（atomic unit），則上式中的電子質量與卜朗克常數都可以設成 1。

即便是 V(-x) = V(x) 這樣的位勢也是可以有各種不同的形狀，在此進一步簡化只做位井的問題，也就是當 x< |a|，V(x) = -V₀、當 x> |a|，V(x) = 0

以下為程式流程概要：

(1) 使用者輸入位井深度 V₀ 與寬度 2a，畫出位井的圖形

(2) 輸入猜測的 E 值，以及奇偶性

(3) 用演算法一步步積分波函數，並繪圖供觀察

(4) 清除畫面、重畫位井、重覆步驟 (2)

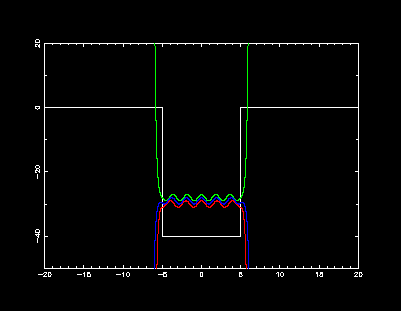
這個程式是供使用者不斷手工嘗試 E 值，找出量子力學允許的那些。

撰寫程式：

（請自行練習）

真的寫不出來，偷看一下老師寫的範例程式

eigen.f eigen.x eigen.f.txt

議題探討：

（請見課文）

時變性薛丁格方程（波包散射）

時變性的薛丁格方程式比非時變的困難得多，從初始時刻 t = t0 開始，每推進一段微小的時間，就要解出整套波函數在空間中的分佈，更麻煩的是，這樣的多變數的解微方問題容易造成不穩定，根本上破壞了解的正確性。我們在這小節因此要學習很保守很穩定的方法，以便處理非時變性薛丁格方程式的積分求解問題。（像是參考書提到我們不應採用 (18.17) 式那種方式的演算法，而應採用 (18.18) 那樣的，細節請見原文）

Gould and Tobochnik 書中採用了另一種方法，它是把時變性波函數（一定有實部與虛部）的實部與虛部分開處理，從原本的薛丁格方程式（以下簡化為一維）

ih d/dt Y(x,t) = -h²/(2m) d²/dx² Y(x,t) + V(x) Y(x,t)

在令

Y(x,t) = R(x,t) + i I(x,t)

拆開成兩組分別處理

d/dt R(x,t) = H_op I(x,t)

d/dt I(x,t) = - H_op R(x,t)

如果在這裏使用半步法（中點法），這種演算法本來是要再多算中點斜率猜測值的（修過數值方法的同學可次回想一下階隆巨庫塔法的策略），但在這裏的狀況成了 I(x,t) 是 R(x,t) 的斜率、-R(x,t) 也是 I(x,t) 的斜率，就可以安排成 R(x,t) 永遠在格子點求值，而 I(x,t) 永遠在中間點求值，如此就都不必多花額外的一倍算求中點斜率了，具的的演算法如下：

R( x, t + Dt ) = R( x, t ) + H_op I( x,t + Dt/2 ) Dt

I( x, t + (3/2)Dt ) = I( x, t + Dt/2 ) - H_op R( x, t + Dt ) Dt

在這種方式的表示下，機率密度 P(x,t) = R(x,t)² +I(x,t)² 仍可以用以下這種方式來表達

P(x,t) = R(x,t)² + I(x,t-Dt/2) I(x,t+Dt/2)

P(x,t+Dt/2) = R(x,t+Dt) R(x,t) + I(x,t+Dt/2)²

Visscher 證明上述演算法在滿足 -2h/Dt < V < 2h/Dt - 2h²/(mDx)² 這樣的 V 與 Dx 值是穩定的 [Ref. Computers in Physics 5(6), 596 (1991)]。

核心演算法提要：

請注意這裹有時間、空間兩個變數，都有被離散化，但在此只有時間是需要做微步推進 Dt 的，Hamiltonian 算符中包含了對空間的二次微分，在那裏相鄰近的空間座標格子間的（波）函數值是有一起作些運算，但不同空間的波函數不是從，而是一開始就給了分佈在整個空間（即空間中處處有定義）的波函數作為初始條件。從演算法上來看，x 點上的波函數值永遠是由上一時刻

試問，新時刻處處的波函數分佈是否仍滿足薛丁格方程式，也就是說

我們是先把空間

撰寫程式