2021 暑期數學 14 講

平面向量（2021.07.17）

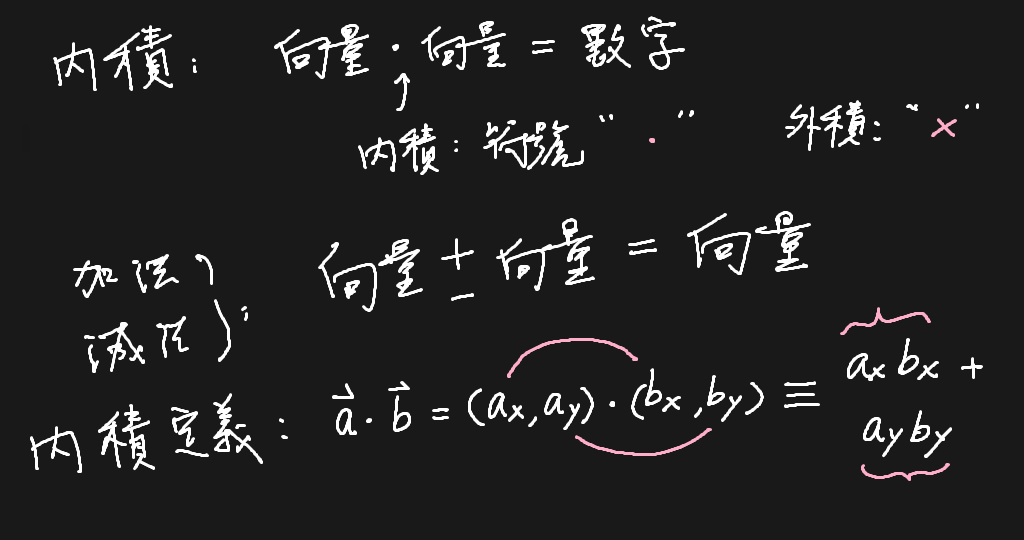
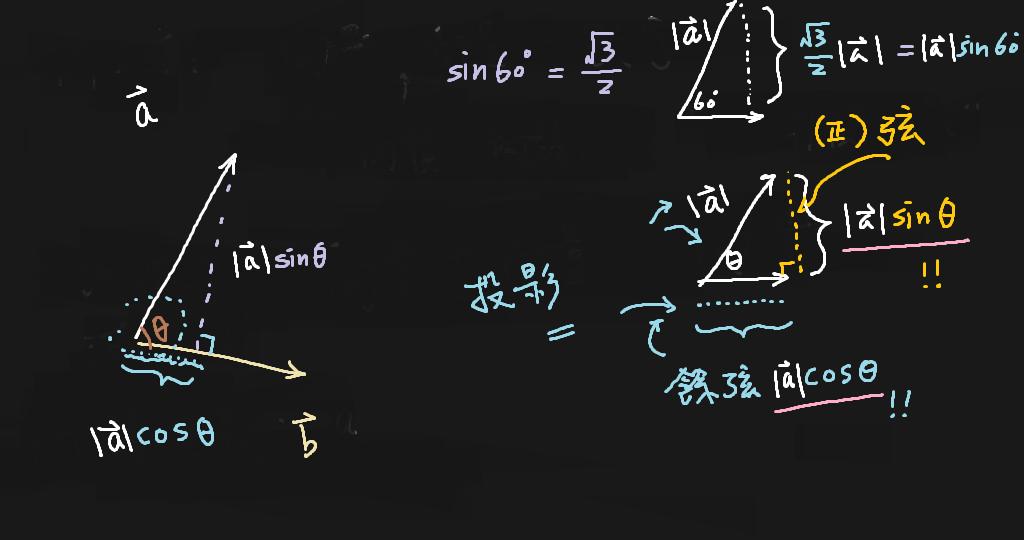
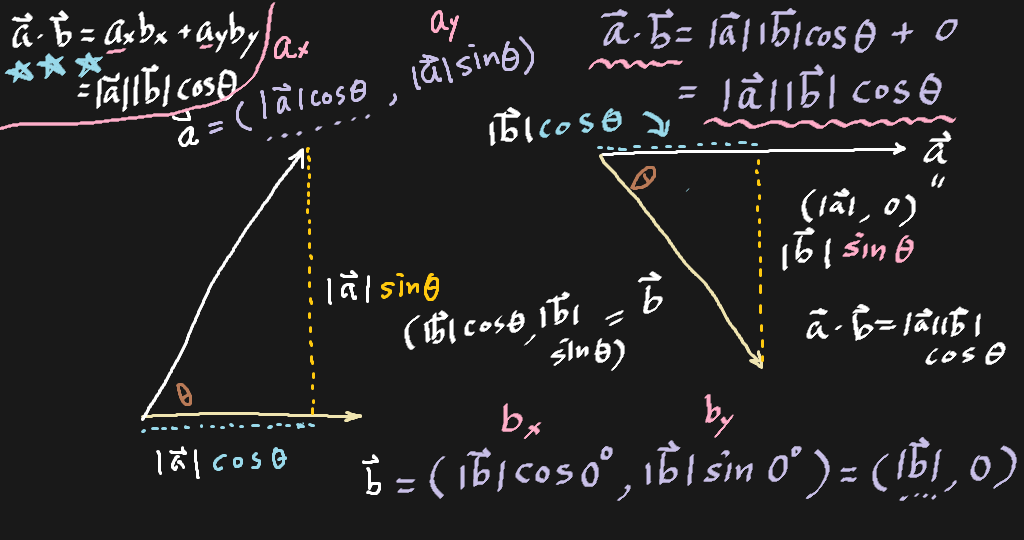
有了內積，便有一個向量間的特殊關係，叫作「正交」。

向量加法，本用於描述一步步位移的總結果，

定正交向量的組合（向量）用來描述平面上的點有用

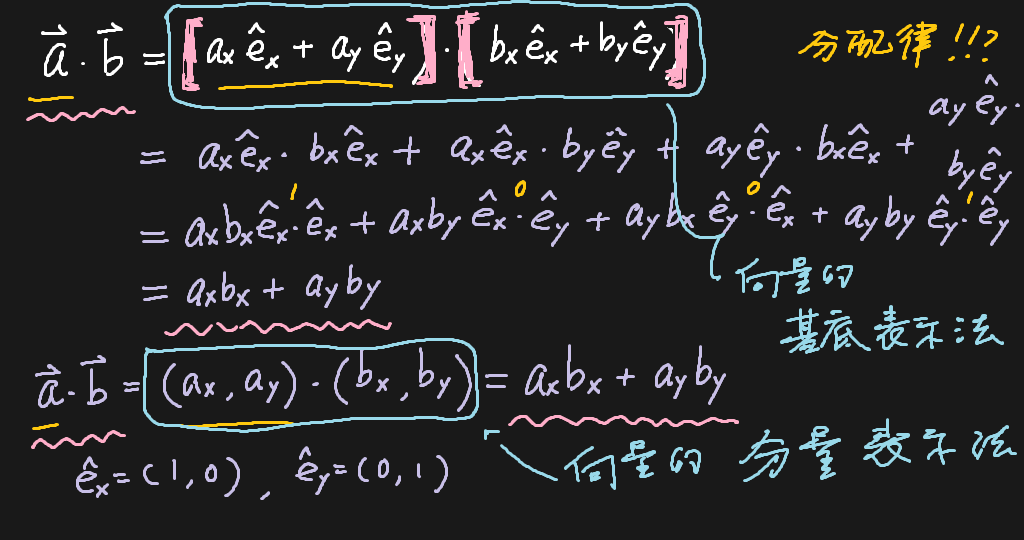
內積、外積，替符號發明規則，讓運算「自動化」！

空間向量

三度空間才能孕育複雜生命，霍金二維狗

 

 

 

 

 

 

 

 

真實的世界，物理的宇宙

運動、力與功，以及動能

位能與力學能

電力線通量

二維及三維矩陣的、行列式值

蹺蹺板如何公平比較？

力矩(可以增加角速度)、角動量

帶電體在磁場中的運動軌跡

平行六面體體積（向量三重積）

 

電流產生磁力線

旋度的數學

因為無窮而有的新數學（數的無盡）

複習：(1)指數律

練習的過程中，發現乘的變加的（用加法來處理相乘的結果，真方便

但一般兩個大任意數相乘，享受不刻每次乘的東西都一樣的這個方便性

有機靈人就想，大數能否分解為多個一樣底數的小一點的值相乘，那兩個大數相乘就方便多了。

實務的問題：3.14159 times 365 = 0.314 times 10^+1 times 0.365 times 10^+2

問：0.314159 是 10^? 3

利用函數關係對應得過去，又原封不動地對應得得回來，上面的問題就是合理的。

從零到一之問的任何數，都給我刻在一張 y = 10^x ，此時 x 是多少 y 需要一個記號來表示，就是 x = log₁₀ y

數學史：對數表的建立（小數後位數越多的越豪華高級）

、

(2) 對數規則、

(3) 計算尺(大數相乘的估算)

背景：分數與小數為什麼可以寫到次方上去？

x^0.3 是什麼怪東西？

答案：只要有 1-1 對應，我們就能毫不混淆地定義 新東西

因為 log( x^0.3 ) = 0.3 log(x) 有明確的雙向可推定義，必致如此、唯因如此 。所以 x^0.3 是有意義的

 

問題：那 i 為什麼可以寫到次方上去？ (有名公式 e^iθ = cosθ + i sinθ )

無限小

無限大

無窮多