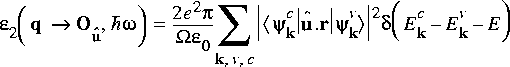微擾理論

量子力學計算與（線性）光學性質預測

從量子力學的計算我們可以獲得系統的總能、單粒子波函數、原子受力等物理量。但是，量子力學計算要如何預測光學性質呢？首先我們必須了解到，各種材料有其特定光學性質，是因為材料皆是由電子與原子核這些帶電粒子所組成，因而會受電磁波的影響，會與電磁波交互作用，。從量子力學的公式來看，引入電磁場兩種方式，的其中一種是電磁波看作是光子，自己也是電子之外的另一種粒子，而粒子之間又有不同的交互作用（透過 hamiltonian）；另一種方法，是把電磁波的效應看作是一種古典的外加場影響。在 CASTEP 中使用的是後者，故看不到光子的波函數，而是會看到 Hamiltonian 中的動量算符被多加了一個向量位（vector potential, A ）。 會具有那樣的形式，是因為如此一來它就會滿足粒子在電磁場下的運動方程式（勞倫斯力）。

微擾理論簡介與非時變一階微擾的結果

要求解上述那樣有新增項 Hamiltonian 的（量子）力學問題，常見的作法是把這個（電磁埸所帶進來的）額外算符項當作是微小的擾動，而用微擾理論的方法來處理。

微擾理論的基本精神，是假設新的物理量與原本被未微擾系統的同一物理量一定有級數展開的關係，以波函數、本徵能量、算符期望值為例：

Ψ = Ψ⁽⁰⁾ + λΨ⁽¹⁾ + λ²Ψ⁽²⁾ + ...

E = E⁽⁰⁾ + λE⁽¹⁾ + λ²E⁽²⁾ + ...

O = O⁽⁰⁾ + λO⁽¹⁾ + λ²O⁽²⁾ + ...

而 λ 則是來自新舊 Hamiltonian

H = H⁽⁰⁾ + λΔH

的關係，其中 ΔH 就是微擾，其大小由 λ 控制。

請注意在這裏 Ψ⁽⁰⁾、E⁽⁰⁾、O⁽⁰⁾、H⁽⁰⁾ 以及 ΔH 我們是知道的，其他上標是 (1)、(2) 等或更高階之各物理量的展開項，我們一開始並不知道，需要從由微擾理論推導整理出來的公式去求解，才能曉得。

至於能讓我們求出解的公式怎麼來的呢？我們有興趣想知道之被微擾系統的解（本徵能量 E 及本徵函數 Ψ），滿足薛丁格方程式

HΨ = EΨ

微擾理論認為前面 λ 展開級數的形式是一定成立的，把 Ψ 及 E 的微擾展開式代入上面的薛丁格方程式。則該式等號的兩邊都會出現一大堆各種次方的 λⁿ 項：

( H⁽⁰⁾ + λΔH ) ( Ψ⁽⁰⁾ + λΨ⁽¹⁾ + λ²Ψ⁽²⁾ + ... )
= ( E⁽⁰⁾ + λE⁽¹⁾ + λ²E⁽²⁾ + ... ) ( Ψ⁽⁰⁾ + λΨ⁽¹⁾ + λ²Ψ⁽²⁾ + ... )

而這個等號關係卻是不管 λ 值是多少，都一定要成立。也就是說，若我們問 λ 的值該是多少，則我們必須要求解依上式移項整理成之 λ 的冪次方式項

Aλ⁰ + Bλ¹ + Cλ² + ... = 0

其中

A = ( H⁽⁰⁾Ψ⁽⁰⁾ - E⁽⁰⁾Ψ⁽⁰⁾ )

B = ( H⁽⁰⁾Ψ⁽¹⁾ + ΔHΨ⁽⁰⁾ -E⁽⁰⁾Ψ⁽¹⁾ - E⁽¹⁾Ψ⁽⁰⁾ )

C = ( H⁽⁰⁾Ψ⁽²⁾ +ΔHΨ⁽¹⁾ - E⁽⁰⁾Ψ⁽²⁾ - E⁽¹⁾Ψ⁽¹⁾ - E⁽²⁾Ψ⁽⁰⁾ )

但是，怎麼可能 λ 無論什麼值都會滿足上面的一元多次方程式呢，唯一的可能，就是 λⁿ 各項的係數 A、B、C、...，都恆等於零。也就是說：

H⁽⁰⁾Ψ⁽⁰⁾ = E⁽⁰⁾Ψ⁽⁰⁾

H⁽⁰⁾Ψ⁽¹⁾ + ΔHΨ⁽⁰⁾ = E⁽⁰⁾Ψ⁽¹⁾ + E⁽¹⁾Ψ⁽⁰⁾

H⁽⁰⁾Ψ⁽²⁾ +ΔHΨ⁽¹⁾ = E⁽⁰⁾Ψ⁽²⁾ + E⁽¹⁾Ψ⁽¹⁾ + E⁽²⁾Ψ⁽⁰⁾

上列各式中之未知數已用顏色標出。

常見有兩種方法(假設無簡併)：

列出 lambda 次方係數另一種的方法，

H⁽⁰⁾Ψ⁽⁰⁾ = E⁽⁰⁾Ψ⁽⁰⁾

( H⁽⁰⁾ - E⁽⁰⁾) Ψ⁽¹⁾ = ( ΔH + E⁽¹⁾ ) Ψ⁽⁰⁾

( H⁽⁰⁾ - E⁽⁰⁾ ) Ψ⁽²⁾ = ( E⁽¹⁾ - ΔH ) Ψ⁽¹⁾ + E⁽²⁾ Ψ⁽⁰⁾

利用 ∫ Ψ^*(0) Ψ⁽¹⁾ dx = 0 的特性（見下註），一階式中，兩側同時左乘 Ψ^*(0) 並積分，等號左側變零，則 E⁽¹⁾ 可直接移項獲得。

註：若 A 是 Hermitian， A | u' > = 0，可證明 < u' | A | u > = 0。證明： < u' | A | u > = < u | A | u' >* = < u | 0 > = 0

求解 Ψ⁽¹⁾ 的方法的，是利用第一式的本徵問題解

H⁽⁰⁾ u_m = E_m u_m

來展開 Ψ⁽ⁿ⁾ 及 E⁽ⁿ⁾，以 Ψ⁽¹⁾ 為例，

Ψ⁽¹⁾ = Σ_n a⁽¹⁾_n u_n

代入前面 λ¹ 係數的式子中，並且假設我們正在處理 Ψ⁽⁰⁾ = u_m 的那組 Ψ⁽¹⁾（當然，其他所有不同 m 值的解也是相同的處理方式），就有（在此以 ΔH_km 代表 <u_k | ΔH | u_m> ）

Σ_n a⁽¹⁾_n E_n u_n + ΔHu_m = E_m Σ_n a⁽¹⁾_n u_n + E⁽¹⁾u_m

自左側乘上n^*_k 並積分，利用 <u_k| u_m> = δ_km，由 k ≠ m 的式子可得

a⁽¹⁾_k = ΔH_km/(E_m - E_k)

注意上式中 k ≠ m （我們正在處理 Ψ⁽⁰⁾_m 的第一階微擾 Ψ⁽¹⁾_m），另外由 m = n 的式子也可順便得

E⁽¹⁾ = ΔH_mm

現在只剩下（正在處理之 m 的）a⁽¹⁾_m 尚未確定，藉由要求 Ψ_m = Ψ⁽⁰⁾_m + λ Ψ⁽¹⁾_m = u_m + λΨ⁽¹⁾_m 必須是歸一化的（取到 λ¹ 的精確度）。則有

1 = < u_m + λ Σ_n a⁽¹⁾_n u_n | u_m + λ Σ_n a⁽¹⁾_n u_n > = 1 + λa⁽¹⁾_m + λa⁽¹⁾_m^* + λ² Σ_n a⁽¹⁾_n a⁽¹⁾_n^*

因為精確度取到 λ¹，因此找到 a⁽¹⁾_m = 0 可以滿足此一情況。到此波函數及能量之一階微擾展開的所有未知係數皆確已定。

至於二階微擾，採用的也是相似的策略，可見於量子物理或量子化學教科書。

簡併微擾

以 Ψ_n⁽⁰⁾ , Ψ_m⁽⁰⁾ 簡併為例，

Ψ_n = C_nnΨ_n⁽⁰⁾ + C_nmΨ_m⁽⁰⁾ + λΨ_n⁽¹⁾ + λ² Ψ_n⁽²⁾ + ...

Ψ_m = C_mnΨ_n⁽⁰⁾ + C_mmΨ_m⁽⁰⁾ + λΨ_m⁽¹⁾ + λ² Ψ_m⁽²⁾ + ...

先對角化 H₀ + λΔH 求新的 Ψ_n 、 Ψ_m

其餘見課本 ......

與時間有關的微擾

黑板推導：費米黃金律

從介電函數虛部出發

介電函數 ε 的定義是 D = ε E，其中 D 是電位移，E 是電場。若把週期變化的電場用複數相量來表示，則實部的介電函數與複數相的電場乘在一起代表波的繼續振動傳播，而虛部的介電函數與複數的相乘在一起則代表有振幅的衰減，就也就意味著介質吸收能量。

電子在單位時間內因吸收電磁波而躍遷的機率，可以由時變性微擾所推導出來的 "費米黃金律" 公式來描述，這代表著介質系統吸收電磁波的情形，它是由電偶極算符、佔據量子態、未佔據量子態、以及這些態的本徵能量差所構成。從電磁波在介質中傳播的觀點，這正是介電常數虛部的行為。因此，介電常數（函數）的虛部透過費米黃金律而能以波函數、本徵能量等量子力學的公式表示出來：

Kramers-Kronig 轉換取得實部

基於物理中的因果關係，介電函數的實部與虛部兩者之間不是各自獨立而是有關。透過 Kramers-Kronig 轉換可得其實部。

要小心的是 K-K 轉換理論上是積分所有頻率範圍，就也就意味著在計算介電函數虛部時，必須引入非常多的空軌域才可能對應到比較高頻率的光子吸收。（至於到底要取多少才夠，須做 "收斂性測試。）

其他（線性）光學物理量

有了實部與虛部的介電函數，就能透過一些簡單的關係其他的線性光學量，例如

吸收係數（吸收光譜）

Abs = ε₂ ω / (n c) ，其中 w 是入射光子頻率、n 是折射率。

折射率

電磁波在介質中傳播的方式可經由折射率來描述，它基本上是描述介質中光線傳播相較於真空中傳播在速率上的差異，此一差異造成了當光線以非垂直角度通過不同折射率物質所構成的介面時，光的行進會彎折一個角度，折射率的名稱由此而來。透明的物質其折射率是純實數，會吸收光線的物質則其折射率虛部不為零。

N = n + ik ，並且 N 與介電函數的關係是 N² = ε = ε₁ + i ε₂