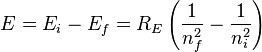Ladders in Atoms：煙火的彩光

 

CO2 狂想曲

C + O2 → CO2 + ΔE

其中各 ΔE 皆為正

C + O2 → CO2 + ΔE1 → ( CO2 ) + ΔE1 → ( C + O2 + ΔE2 ) + ΔE1 → ( C + O2 ) + ΔE2 + ΔE1 → ( CO2 + ΔE1 ) + ΔE2 + ΔE1

其中各 ΔE 皆為正

不可能，

表示這是一種狀態、一種位能（只與狀態有關）。既然這是一種位能，

 

為什麼 2H2O 比 2H2 + O2 能量（位能）低，而不是

 

 

煙火的彩光

 

 

原子內的能階

Balmer 與氫原子光譜

光譜儀分解出 複雜的 氫原子光譜。

瑞典中學教師 Balmer 用藝術般的方式把 頻率擬合到精準的公式規則上

v = R' ( 1/22 - 1/n2 )

其中 R' 來自光譜本身。他甚至認為這是另一個更一般性公式

v = R' ( 1/n12 - 1/n22 )

的特殊情況。

E=E_i-E_f=R_E \left( \frac{1}{n_{f}^2} - \frac{1}{n_{i}^2} \right) \,

進個公式懸而未解 30 年。

原子是穩定的

從實際的經驗，原子是穩定存在的事實，電子沒有塌陷到原子核上

 

波爾模型 (1913)

系統有能階，電子在能階間跳躍。

E3 = Rω2 （束縛能的古典公式）

E = nα h ω（電子必須遵從的額外指令）

E1 - E2 = h ν

前兩式合併消除 角頻率 ω，得

E = R / (α2 h2 n2)

再將上式束縛能寫成 E1、E2 並相減，得

 

hv = R/(α2 h2)  ( 1/n12 - 1/n22 )

最後得（用了對應性論述，要求 α 必需是 1/2 )

v = 4R/ h3  ( 1/n12 - 1/n22 )